ロジットモデルとプロビットモデル

某授業でロジットモデルとプロビットモデルの説明を求められたので、ここにメモ。

ロジットモデルとプロビットモデルは、従属変数がカテゴリカルなデータである時に用いられる分析手法である（ただし、特に計算が簡単なロジットモデルについては、よく知られている多項ロジット、二項ロジット、順序ロジット以外にも色んなモデルが提案されている！この辺りについては、また機会があればまとめたい）。

そもそも、なぜカテゴリカルな従属変数に対して、普通の線形回帰が用いられないかというと、

①誤差が正規分布しない

②予測値がおかしくなってしまう

③誤差が均一分散しない

といった理由がある。

①の誤差が正規分布に従うのは、回帰係数のt検定の時に必要な前提である。

②は、例えば、1 or 0の従属変数に対して通常の回帰分析を行うと、回帰係数の値によっては予測値が1より大きくなったり、0より小さくなったりと意味がわからなくなってしまう。

③の誤差の均一分散の仮定は、効率性のための重要な前提である（この辺り、経済学分野の人はめちゃくちゃ敏感だが、他の分野の人は気にしていない傾向にあるが…）

そこで、ロジットモデルおよびプロビットモデルが使用される。この両者の違いは、はっきり言って好みの問題のような気がする。経済学分野の人はプロビットモデル、社会学分野の人はロジットモデルを好む傾向にある。サンプルがある程度大きければ、有意性検定や回帰係数の符号はそこまで変わらないと思われるので（今度実験する）、どっち使っても良いのではないかと…。私は、解釈のしやすさ、応用性の観点から、ロジットモデルの方が好きである。後でみるように、式もすっきりしているし分かりやすい。

厳密に言うと、両者の違いは、カテゴリカルな従属変数の背後にある潜在的な従属変数を仮定したときに、その潜在的な従属変数に対するモデルの誤差が従う確率分布を、正規分布（プロビットモデル）、ロジスティク分布（ロジットモデル）にするかの違いがある。

前置きは、このくらいにして、ロジットモデルとプロビットモデルについて、よりしっっかりと説明する。なお、ここでは簡単のため、二項ロジットモデルおよび二項プロビットモデルについて説明する。ただし、ここでの説明の発想は、多項ロジット（プロビット）、順序ロジット（プロビット）においても同一である。

まず、2値変数の従属変数を考える。例えば、トマトが好き=1、トマトが嫌い=0とする。

ここで、トマトの好き嫌いを決定する連続的な潜在変数を考える。すなわち、「トマトの好き度」みたいな尺度を考える。この「トマトの好き度」が0以上の場合は、トマトが好きと答え、「トマトの好き度」が0未満の場合は、トマトが嫌いと答えると想定する。

それで、この連続量である「トマトの好き度」に対して、普通の回帰分析を行うようにモデルを組む（なお、簡単のため独立変数は1つにする）。

以上を式にすると以下の通りである。

$y*=α+βx+e$

$y=1(ify*≧0)$

$y=0 (if y*＜0)$

ここで、y*は「トマトの好き度」、yはトマトが好き（=1）orトマトが嫌い（=0）を表している。なお、y*は潜在的な変数で誰にも観測されない。ただ単に、モデルとしてそのような潜在的な変数が存在していると仮定しているだけである。

ここで、y=1になる時の確率 $p_1$ を考える。

上の式から、 $p_1$ は以下のようになる。

$p_{1}=Pr(y=1)=Pr(y*≧1)=Pr(-(α+βx)≦e)$

ここで、eを標準ロジスティック分布もしくは標準正規分布に従うとする。その確率はそれが従う確率分布の密度として表現できる。よって、累積分布関数で表現できる。ここで、その累積分布関数をF( . )として表現すると、上記の式は以下のようになる（なお、以下の式変換では、標準ロジスティック分布も標準正規分布も左右対称であることに留意）。

$Pr(-(α+βx)≦e)=1 - F(-(α+βx))=F(α+βx)$

ここで、F( . )が標準ロジスティック分布の累積分布関数である場合は、F( . )は以下のように表現される。

$F(e)=\int_{-∞}^{e}\frac{exp(e)}{(exp(e)+1)^2}⇄F(e)=\frac{1}{1+exp(-e)}⇄F(e)=\frac{exp(e)}{exp(e)+1}$

一方で、 F( . )が標準正規分布の累積分布関数である場合は、F( . )は以下のように表現される。

$F(e)=\int_{-∞}^{e} {\frac{1}{\sqrt{2π}}exp(-\frac{y^2}{2})}dy$

このように、eが標準ロジスティック分布に従うとした場合は、ロジットモデル。eが標準正規分布に従うとした場合は、プロビットモデルとなる。

なお、 y=0になる時の確率 $p_0$ は $p_{1}+p_{0}=1$ から、以下のように表現できる。

$p_0 = 1-F(α+βx)$

以上の手続きから、y=1になる確率 $p_{1}$ およびy=0になる確率 $p_{0}$ は累積分布関数を使って、以下のようにきれいに表現できることがわかる。

$p_1 = F(α+βx)$

$p_0 = 1-F(α+βx)$

F(α+βx)は-∞からα+βxまでの密度であるので、αもしくはβが大きくなればなるほど、その密度が増加する。すなわち、 $p_{1}$ となる確率が大きくなり、 $p_{0}$ となる確率が小さくなる。このイメージとしては、以下の通りである。

f:id:abcxyzonetwothree:20181124134905p:plain

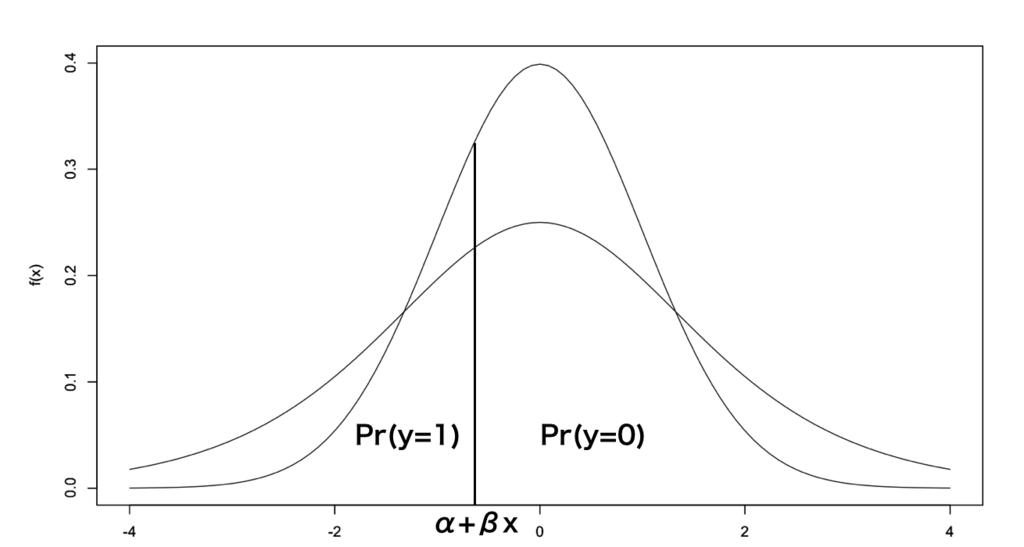
山が小さい方がロジスティック分布、山が大きい方が正規分布である。α+βxが大きくなればなるほど、 $p_1$ が大きくなり、 $p_0$ が小さくなる。

すなわち、何らかの独立変数xの係数βが正であるならば、独立変数がx増加すると、β分だけ $p_1$ が大きくなると解釈できる（厳密に言うと、この表現は間違っていて、F( . )を外す操作が必要です！ただし、分かりやすさのためにこのように表現している）。

なお、αおよびβの推定方法は最尤法を用いる。例えば、id1の人のxが3点でトマトが好きと答えた場合 $p_{11}=F(α+3β)$ 、id2の人がx=5でトマトが好きと答えた場合 $p_{12}=F(α+5β)$ 、id3の人がx=2でトマトが嫌いと答えた場合、 $p_{03}=1-F(α+2β)$ …という手順で全ての人の確率pを表現する。これらの人たち（N人）が全くランダムにサンプルされたならば、これらの現象は互いに独立なので、以下のように尤度関数が表現できる。

$L = \prod_{i=1}^{N}p_{1 or 0}^{i}$

この尤度関数を最大化するαとβがロジットモデルもしくはプロビットモデルでの推定値となる。

ここで、簡単なデータで二項ロジットモデルを、マニュアルで行なってみた。

使用するデータは以下の通り。

f:id:abcxyzonetwothree:20181124140414p:plain

このデータに対してyを従属変数、xを独立変数とした場合、二項ロジットモデルを適用すると、以下の尤度関数を最大化するαとβが計算される。

$L(α, β) =( 1-\frac{exp(α+β2)}{exp(α+β2)+1})×( 1-\frac{exp(α+β6)}{exp(α+β6)+1})×( 1-\frac{exp(α+β9)}{exp(α+β9)+1})×\frac{exp(α+β5)}{exp(α+β5)+1}×\frac{exp(α+β1)}{exp(α+β1)+1}×( 1-\frac{exp(α+β8)}{exp(α+β8)+1})×\frac{exp(α+β3)}{exp(α+β3)+1}×\frac{exp(α+β7)}{exp(α+β7)+1}×( 1-\frac{exp(α+β4)}{exp(α+β4)+1})×\frac{exp(α+β10)}{exp(α+β10)+1}$

本当は、偏微分を用いて、上記の尤度関数を最大化するαとβを求めるのであろうが、分かりやすくするため、αとβに-2.999から3.000まで0.001ずつ増加させた数をそれぞれ代入してその中でL(α,β)が最大となったα、βを求める。すなわち、下記の表のようにして、Lが最大となったαとβを取り出す。

f:id:abcxyzonetwothree:20181124140922p:plain

その結果、L=0.001031491が最大値となった。その時の、αとβはそれぞれ、0.401、-0.073であった。

次に、Rのglm()を用いて、二項ロジットを回してみると、α=0.4026、β=-0.0732となった。

ほとんど同じ結果となった！少し異なるのは、代入するαとβの値が粗いためだと考えられる。

なお、その尤度関数を3Dプロットすると以下のようになる（代入するαとβはだいぶ粗くしている。なぜなら、細かくするとパソコンが固まってしまうため）。

RPubs - Likelihood

以上である。今回使ったコードは以下の通り。

 ##ロジスティック分布と正規分布の図示
curve(dnorm,from=-4,to=4,ylim=c(0,0.4),ylab="f(x)")
par(new=T)
curve(dlogis,from=-4,to=4,identity=T,,ylim=c(0,0.4),ylab="f(x)")


#擬似データ作成
x<-c(2,6,9,5,1,8,3,7,4,10)
y<-c(0,0,0,1,1,0,1,1,0,1)
data0<-data.frame(x,y) 

#y=1となるときの確率p1と、y=0となるときの確率p0
p1<-function(a,b,x){(exp(a+b*x))/(1+exp(a+b*x))}
p0<-function(a,b,x){1-((exp(a+b*x))/(1+exp(a+b*x)))}

#尤度関数
L<-function(a,b){
  p0(a,b,data0[1,1])*p0(a,b,data0[2,1])*p0(a,b,data0[3,1])*p1(a,b,data0[4,1])*p1(a,b,data0[5,1])*p0(a,b,data0[6,1])*p1(a,b,data0[7,1])*p1(a,b,data0[8,1])*p0(a,b,data0[9,1])*p1(a,b,data0[10,1])
}

#-2.999~3までの数字を0.001ずつ増加させた数の羅列を6000回繰り返す
a<-rep((-2999:3000)/1000,6000)
b<-rep((-2999:3000)/1000,each=6000)
data_ab<-data.frame(a,b)

#a, b, L(a,b)のそれぞれの値の表から、Lが最大値となる場合のa,bを取り出す
L<-L(a,b)
data<-data.frame(L,a,b)
which.max(data$L)
data[which.max(data$L),]

#二項ロジット
glm(data0$y~data0$x,family=binomial)


##3Dプロットのためにデータ簡略##

#擬似データ作成
x<-c(2,6,9,5,1,8,3,7,4,10)
y<-c(0,0,0,1,1,0,1,1,0,1)
data0<-data.frame(x,y) 

#y=1となるときの確率p1と、y=0となるときの確率p0
p1<-function(a,b,x){(exp(a+b*x))/(1+exp(a+b*x))}
p0<-function(a,b,x){1-((exp(a+b*x))/(1+exp(a+b*x)))}

#尤度関数
L<-function(a,b){
  p0(a,b,data0[1,1])*p0(a,b,data0[2,1])*p0(a,b,data0[3,1])*p1(a,b,data0[4,1])*p1(a,b,data0[5,1])*p0(a,b,data0[6,1])*p1(a,b,data0[7,1])*p1(a,b,data0[8,1])*p0(a,b,data0[9,1])*p1(a,b,data0[10,1])
}

#-2.9~3までの数字を0.1ずつ増加させた数の羅列を60回繰り返す
a<-rep((-29:30)/10,60)
b<-rep((-29:30)/10,each=60)
data_ab<-data.frame(a,b)

#a, b, L(a,b)のそれぞれの値の表から、Lが最大値となる場合のa,bを取り出す
L<-L(a,b)
data<-data.frame(L,a,b)
which.max(data$L)
data[which.max(data$L),]

#図示する
library(plotly)
g<-plot_ly(data=data, x=b, y=a, z=L,size=1)
print(g)